Gamma-ray spectroscopy at MHz counting rates with a compact LaBr₃ detector and silicon photomultipliers for fusion plasma applications

As magnetic fusion science matures towards the exploitation of high power tokamak devices, there is a pressing demand to better understand the role played by the energetic ions in the sustainment of the thermonuclear process.¹ From the experimental point of view, this calls for the need to develop dedicated diagnostic systems that can be operated in the harsh, neutron rich environment of a high performance tokamak. As mostly demonstrated at the Joint European Torus (JET), neutron and gamma-ray spectroscopy measurements are among the primary techniques for fast ion studies in plasmas of deuterium and deuterium-tritium at high power. Neutron measurements can especially diagnose supra-thermal components of the fuel ion energy distribution by observation of the corresponding high energy tails in the spectrum.^2–4 Gamma-rays are instead the main tool to study the charged energetic products of the fusion reactions.^5–10 

In view of the forthcoming full power deuterium-tritium campaign, a number of diagnostics are undergoing major upgrades at JET. The gamma-ray camera,^5,11 i.e., a multi-chord system aimed at determining the map of the gamma-ray emissivity in the poloidal plane by tomographic inversion, is among these and is expected to be the main instrument that will determine the α particle profile by measurements of the gamma-ray emission at 4.44 MeV from ⁹Be(α, nγ)¹²C reactions in the plasma (at JET ⁹Be comes from erosion of the machine first wall). The requirements for operating the detectors of the gamma-ray camera at full power are however very demanding. Space limitations constrain the detectors to fit a cylindrical capsule of 35 mm × 35 mm (height x diameter). There is then need for MHz counting rate capabilities, insensitivity to magnetic fields, and a peak energy resolution of 3%-4% in the 3-5 MeV range. No detector that can simultaneously satisfy these requirements is commercially available.

A dedicated instrument, based on a LaBr₃ crystal combined with silicon photo-multipliers (commercially known as Multi-Pixel Photon Counter, MPPC), has been developed to meet all of these requirements. Its detailed design and characterization in the laboratory are described elsewhere in these proceedings.¹² In this paper, we focus instead on the first time demonstration of gamma-ray spectroscopy measurements at MHz counting rates with this type of detector. The measurements were obtained in an experiment at a tandem nuclear accelerator, where counting rates up to 2.9 MHz could be reached.

The paper is organised as follows. The measurement setup and data analysis procedure are described in Section II. Gamma-ray spectra obtained in our experiment and their characterisation in terms of peak shift and energy resolution are presented in Section III. Implications of our findings and routes for further improvements are finally addressed in Section IV.

High counting rate gamma-ray spectroscopy measurements were performed at the TANDEM-ALPI accelerator of the Italian Institute of Nuclear Physics in Legnaro. A beam of 10 MeV protons was collimated onto a target of ²⁷Al placed in a cylindrical vacuum chamber. The MPPC detector was installed inside the chamber and at a distance of less than 1 cm from the target. The thickness of the target was chosen to fully stop the proton beam and maximise gamma-ray production. This arose from either inelastic proton scattering on aluminium or the ²⁷Al(p, αγ)²⁴Mg nuclear reaction. A photo-multiplier tube (PMT) equipped with a 1″ × 1″ LaBr₃ detector was placed outside the vacuum chamber and at a distance of about 20 cm from the target. This second detector, whose counting rate never exceeded 250 kHz at the highest proton currents we have used (30 nA), was used to benchmark the determination of the counting rate on the MPPC detector (see the description below).

The raw signals from both the PMT and MPPC were digitized with a CAEN DT5730 digitizer (500 MHz, 14 bits, 2 V dynamic range), without any intermediate amplification stage. In this way, the duration of the electronic signal from a gamma-ray event was about 100 ns, which is essential to limit the extent of pile up for spectroscopy measurements at MHz counting rates.^13–15 When a pulse exceeded a chosen threshold, corresponding to an energy around 500 keV, a trigger was launched and a window of 300 ns was opened to digitise signals from the PMT and MPPC occurring within the window. The MPPC was operated at 65.8 V, which is 0.6 V above the breakdown voltage (see Ref. 16). The energy spectrum was reconstructed after each measurement based on the interpolation procedure described in Ref. 13. To this end, we fitted each digitised waveform with the expected pulse shape y(t) from a silicon photomultiplier,¹⁷ i.e.,

where τ₁ = 30.4 ns and τ₂ = 22.6 ns were constant for all waveforms and A, N, and t₀ were instead determined by the fit. The resulting fit parameters were used to calculate the pulse height of each event and build the energy spectrum. A standard pile up rejection routine was applied before fitting so to discard events that had more than one pulse within a single 300 ns acquisition window.

An essential quantity for our experiment was the counting rate r on the MPPC which, due to pile up, does not always coincide with the number of triggers per unit time, especially at the highest detector loads. We have thus determined r by averaging the number of pulses recorded in several acquisition windows lasting 1 μs and launched before each measurement of the spectrum without any energy threshold. In order to benchmark our determination, we have further verified that, as the beam current was increased, r remained proportional to the rate of the external PMT monitor, which was exposed to a 10 times lower radiation load. Counting rates between 52 kHz and 2.9 MHz on the MPPC detector were assessed in our experiment.

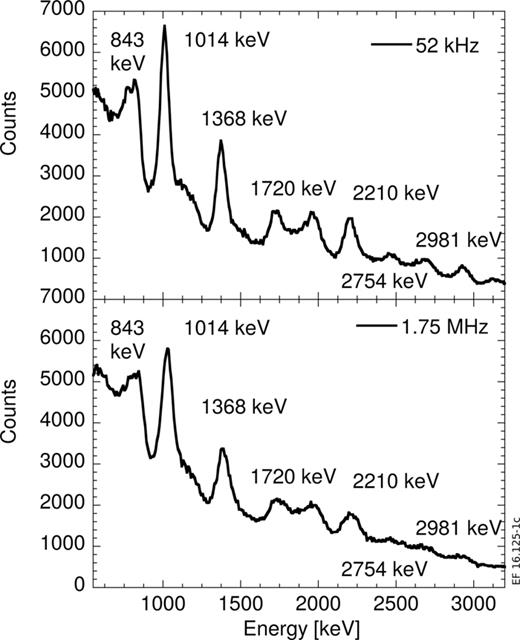
Figure 1 shows the gamma-ray energy spectra measured at counting rates of 52 kHz and 1.75 MHz. Even when r is as high as 1.75 MHz, we are able to resolve all of the peaks marked in the figure and observed at the more moderate rate of 52 kHz. The main difference between the two spectra is mostly in terms of the energy resolution, which appears to be coarser at high counting rates. The gamma-ray peaks we have identified sit on an exponential background that is significantly more pronounced in the MHz range. This is due to the activation of the vacuum chamber where the experiment was performed and which increases at the highest proton beam currents.

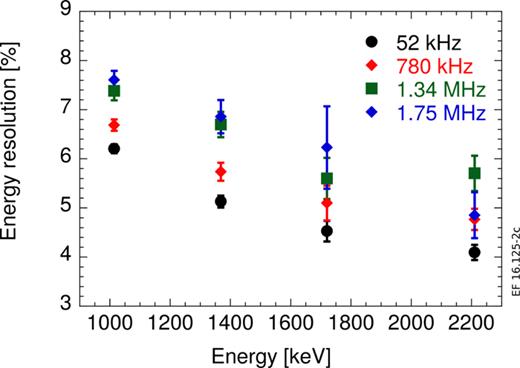
As the energy resolution is an important parameter for our goal, we have quantified its changes as a function of r, with the results shown in Figure 2. The resolution (%) is here defined as the ratio between the width and position of each peak. The error bar associated to E_γ = 1720 keV is largest as this energy had the worst peak to background ratio. We also did not try to extract values at the 2754 and 2981 keV peaks, as they barely stand out of the background at 1.75 MHz. Unlike the measurement in Ref. 13 with a 3″ × 6″ LaBr₃ scintillator and a PMT, we here observe a clear change of the energy resolution between 1% and 2% at all peaks. However, we have verified that, at a given counting rate, the energy resolution predominantly scales as $1/ E γ$⁠, as expected from Poisson statistics. This implies that we can extrapolate a value between 3% and 4% at the 4.44 MeV peak from the ⁹Be(α, nγ)¹²C reaction at r = 1.75 MHz, which is deemed sufficient to distinguish this emission from nearby lines, with mean energies typically separated by a few hundreds keV.

A second aspect that is worth mentioning is the observed downward shift of the mean peak position as a function of r and illustrated in Figure 3. As shown in the right panel, the relative shift increases with the counting rate, but is independent from the gamma-ray energy. This suggests that the increasing average current flowing in the device, 〈I_S〉, which scales linearly with r, affects the gain of the MPPC. In particular, by analysing time resolved data, we were able to separate two contributions to the peak shift. The first contribution was manifested from the beginning and comes from an additional voltage drop along the resistors of the MPPC electronic board.¹² This is due to 〈I_S〉 and reduces the effective gain of the MPPC. Since 〈I_S〉 is also a source of local heating for the device, there is then a second contribution that comes from the increase of the local temperature, which further reduces the MPPC gain,¹⁶ and occurs until thermal equilibrium is reached on a time scale of a few seconds. In Figure 3, we only show the first, unavoidable contribution to the shift, as the latter can be counteracted by real time control of the MPPC gain with a temperature sensor¹⁸ or by time resolved measurements. The energy resolutions reported in Figure 2 were instead evaluated by integrating our measurements over a time window after the MPPC had reached thermal equilibrium.

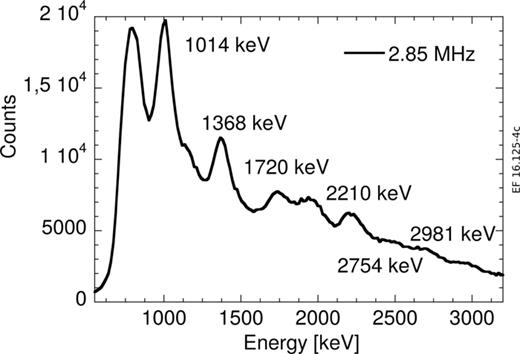
As a final test of the capability of our device to operate at high counting rates, we finally increased the proton beam current up to 30 nA, which was the highest value allowed by radiation protection limits and corresponded to 2.9 MHz on the MPPC detector. We also decided to operate the device at 65.5 V, i.e., only about 0.3 V above the break down. The resulting spectrum is displayed in Figure 4 and shows that all of the peaks can still be distinguished, but at the price of an overall worsened energy resolution (7% at E_γ = 2210 keV) and a significantly higher background from the activation of the vacuum chamber. Even higher counting rates may be sustained by the device, which provides additional confidence on the detector capability to perform spectroscopy measurements in the MHz range.

Gamma-ray measurements of the 4.44 MeV peak from the ⁹Be(α, nγ)¹²C reaction in deuterium-tritium plasmas must always be accomplished in a high background of 14 MeV neutrons, which are born from the main fusion reactions. 14 MeV neutrons interact with the LaBr₃ crystal^19,20 and induce a direct background that can be reduced by the use of suitable attenuators, but that cannot be fully suppressed. Preliminary calculations for a JET deuterium-tritium plasma reveal that a detector load of the order of 1 MHz, mostly with events at E_γ < 3 MeV, may be expected in a full power deuterium-tritium discharge from the 14 MeV neutrons, with a contribution of about 1-10 kHz from ⁹Be(α, nγ)¹²C reactions at 4.44 MeV. As discussed in Ref. 13, the effect of the radiation load on the detector depends on the average current flowing in the device, which is in turn proportional to the product between the average energy of the measured spectrum, 〈E_γ〉, and the counting rate. From Figure 1 we can calculate 〈E_γ〉 ≈ 0.65 MeV for our measurements and that compares to 〈E_γ〉 ≈ 0.68 MeV for 14 MeV neutrons impinging on the LaBr₃ crystal we have used. As we were able to successfully measure the spectrum from p + ²⁷Al reactions up to 2.9 MHz, this implies that a correspondingly high detector load may be tolerated in a measurement at JET.

Although our measurements already demonstrate the technical feasibility of α particle measurements by gamma-ray spectroscopy in a JET deuterium tritium plasma, further improvements may be envisaged. An example is the energy resolution that, at kHz counting rates, has an optimum at about 3 V above the MPPC breakdown^16,17 so that, depending on the actual extent of the 14 MeV neutron background in each plasma scenario, operations at higher MPPC voltage (and correspondingly better energy resolution) may be feasible. In our measurements, we did not seek to obtain the optimal energy resolution, but rather to show that spectroscopy measurements at MHz counting rates could be performed at an energy resolution sufficient for our scope.

A second amelioration may then come from the use of an active circuit for signal read-out from the MPPC, for example, based on a transimpedance amplifier circuit (TIA) instead of a passive differentiator circuit as in our measurements.^12,18 Laboratory tests¹⁸ have shown that a TIA circuit can minimise the gain shifts due to the average current in the device, but with the need of an additional power supply to feed the operational amplifier of the TIA. High counting rate tests of a CeBr₃ detector coupled with an MPPC and TIA readout were also performed in our experiment and will be reported in a separate paper.

Gamma-ray spectroscopy measurements from p + ²⁷Al reactions at counting rates from 50 kHz up to 2.9 MHz were successfully performed for the first time with a compact LaBr₃ detector and a silicon photo-multiplier readout. In all cases, we were able to successfully reconstruct all of the peaks expected from the reactions and with an energy resolution that extrapolates to 3%-4% in the E_γ = 3-5 MeV range of interest for fast ion studies with gamma-ray spectroscopy at JET. An increasing downward shift of the mean peak position as a function of the counting rate was also observed, as expected, but this is of no concern as it can be counteracted by time resolved measurements at JET.

Our results demonstrate the technical feasibility of spectroscopy measurements with the JET gamma-ray camera upgrade in forthcoming deuterium-tritium plasmas at high performance and, more generally, show that good energy resolution, MHz rate capabilities, insensitivity to magnetic fields, and compact dimensions can all be combined within a single gamma-ray spectrometer.

This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014-2018 under Grant Agreement No 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.